Как определить погрешность выборки в соцопросе

Чаще всего именно системную ошибку измерения называют погрешностью выборки. Значит, для определения погрешности выборки надо определить системную ошибку измерения. Последние годы я применяю достаточно простую методику для того, чтобы определить систематическую ошибку измерения, полученную в ходе социологического опроса.
На самом деле определение погрешности выборки — дело нетривиальное. Для того, чтобы определить погрешность выборки, надо какое-то значение генеральной совокупности (к примеру, рейтинг) сравнить с этим же значением в выборке. Но мы же проводим выборочное исследование для того, чтобы по данным выборке судить о данных всей генеральной совокупности и в данном случае погрешность должна сказать, насколько сильно значение во всей генеральной совокупности может отличаться от выборочного. Получаем уравнение с двумя неизвестными.
Давайте разбираться в ситуации.
Говорить об ошибке выборки для всего опроса не совсем корректно. Под ошибкой понимают разницу между показателем какого-либо признака в генеральной совокупности и в выборке. Таким образом, для каждого признака надо говорить о своей погрешности. Высказывание «погрешность опроса» чаще всего бывает бессмысленным, лучше говорить о «погрешности вопроса». Но моя методика как раз подходит для практически всего исследования.
В политических исследованиях, да и в коммерческих тоже, мы чаще всего имеем дело с бинарными вопросами, то есть вопросами, на который дается ответ «да» или «нет». Классический рейтинговый вопрос «За кого бы Вы проголосовали, если бы выборы состоялись в ближайшие выходные?» — частный случай бинарного вопроса. Его можно представить как несколько вопросов о поддержке каждого кандидата или партии: «Если бы выборы проходили в ближайшие выходные, проголосовали бы вы за кандидата N***?» и два варианта «Да, проголосовал» и «Нет, не проголосовал».
В статистике для оценки погрешности биноминального распределения используется следующая формула:
где Sbin — ошибка биноминального распределения
p — процент наблюдений (рейтинг)
n — размер выборки.
Максимального значения ошибка достигается, когда p=50%, то есть пополам ответили «да, проголосовал бы» и «нет, нет не проголосовал бы». Во всех остальных случаях ошибка меньше. Мы можем оценить ошибку взяв максимальное значение.
На следующем шаге мы воспользуемся правилом «Двух сигм» (или, по желанию, правилом «Трех сигм»). Правило говорит, что 95% всех значений распределения укладываются в интервал
В этом случае ошибку, согласно правилу «двух сигма» при 95%-ном доверительном интервале равна ±2*Sbin. В итоге мы получаем формулу, с помощью которой можно оценить ошибку выборки при 95%-ном доверительном интервале и ошибка будет зависеть только от размера выборки:
Где ε — погрешность выборки, n — размер выборки.
Получаем, что для выборки в 1000 человек погрешность измерения составит 3% при 95%-ном доверительном интервале.

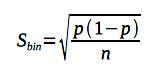
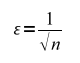











1 Comment